Skip to main content
Featured

How to Calculate your Price Range on Uniswap v3

Brandon Ly

How do you LP on Uni v3 with a ±% range? E.g. if you wanted ±30% should you do:

  • Lower: P⋅70%\text{Lower: } P \cdot 70\%
  • Upper: P⋅130%\text{Upper: } P \cdot 130\%

or

  • Lower: P1.3\text{Lower: } \frac{P}{1.3}
  • Upper: P⋅1.3\text{Upper: } P \cdot 1.3

Let's find out! 👇

The upper price is the same since P⋅130%=P⋅1.3P \cdot 130\% = P \cdot 1.3. But what about the lower price? Should it be 70% or 76.9%? (76.9%=11.376.9\% = \frac{1}{1.3})

It turns out that only one of these is correct! Let's analyze.

  • Pool: ETH-USDC
  • Price: $1,528
  • Our capital: split evenly (1 ETH and 1,528 USDC)

Let's try method 1 for a ±30% range: LP between 70% ($1,069) and 130% ($1,986).

Spoiler alert: we can’t! When we go to Uniswap it won’t let us LP all our capital. In fact, it will only let us deposit 0.75 ETH. That's 14\frac{1}{4} of our ETH not earning any yield!

img-1

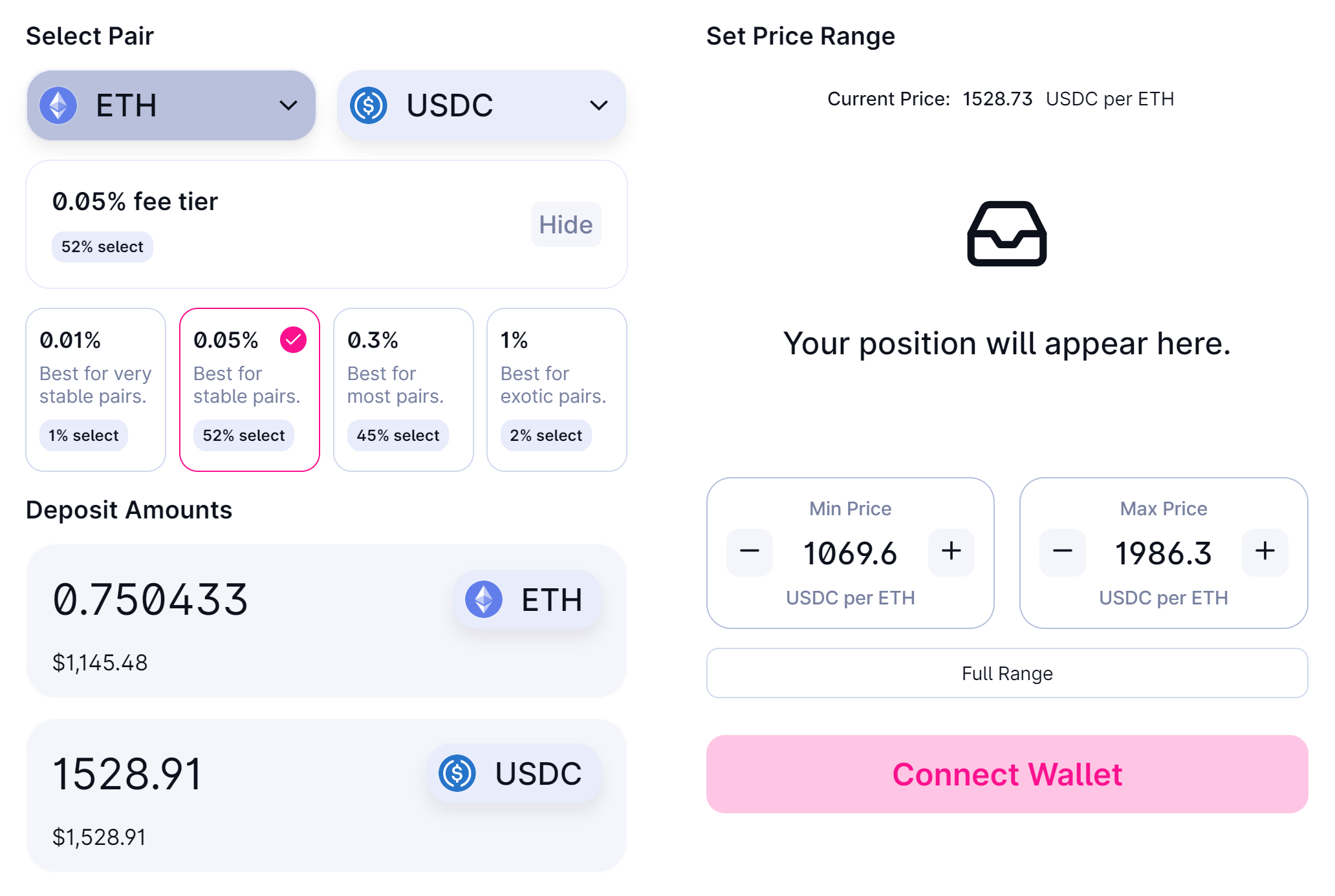
Now let's try method 2.

Since 11.3=76.9%\frac{1}{1.3} = 76.9\% and 1.3=130%1.3 = 130\%, we LP between 76.9% (~$1,176) and 130% ($1,986).

Uniswap lets us deposit all our capital. Success!

img-2

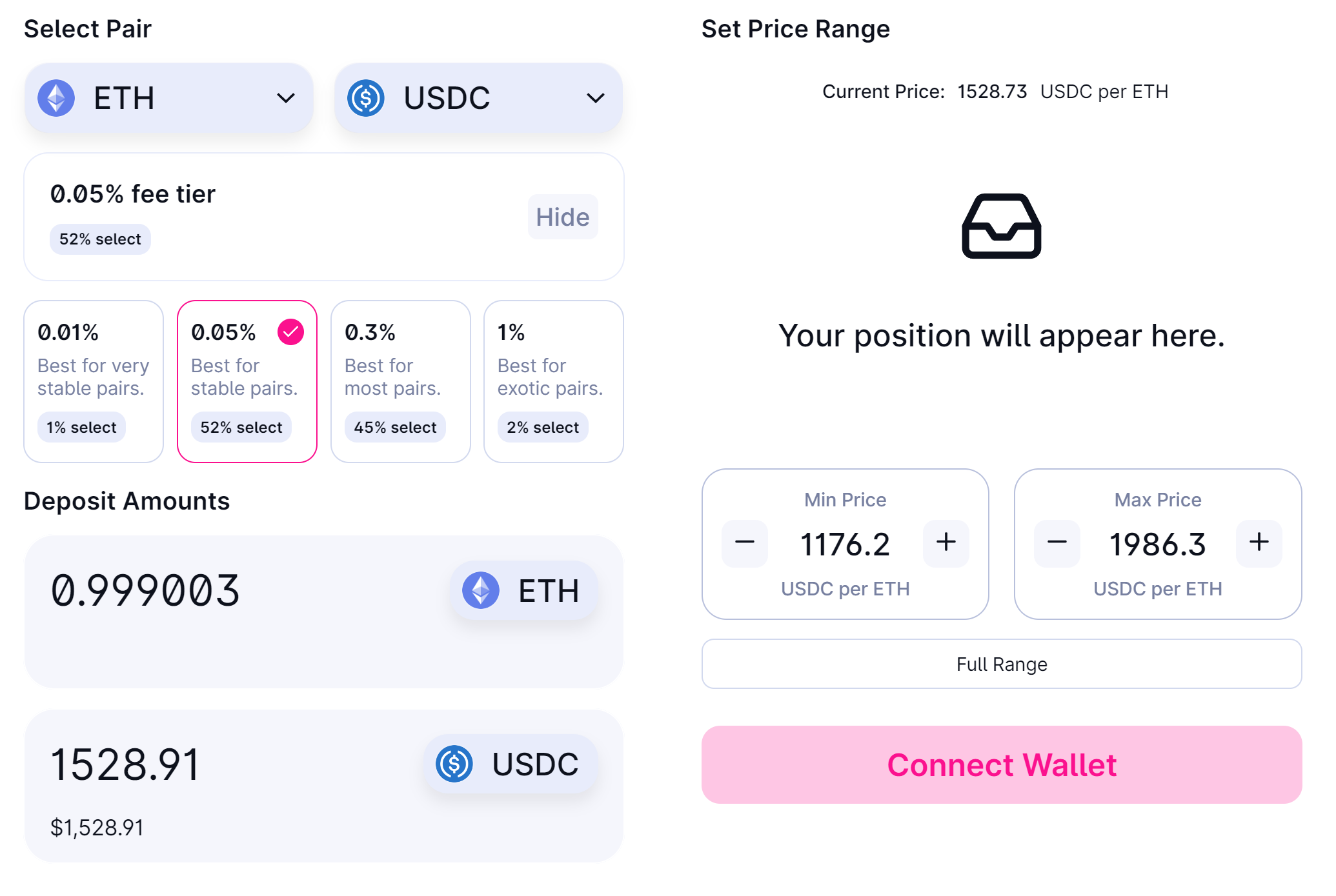
So why is the lower range P1.3\frac{P}{1.3} rather than P⋅70%P \cdot 70\%?

It turns out that we have to follow the equation:

lowerP=Pupper\frac{lower}{P} = \frac{P}{upper}

E.g. if the lower range is 23\frac{2}{3} of P, then P must be 23\frac{2}{3} of the upper range. See @atiselsts paper (3.2.2) for more here.

This seems unintuitive 🤔 Why can’t we simply do ±30% of P?

The answer is that we are working with tick math, which involves exponents. So LP ranges are linear in “tick space”, but non-linear in “price space”. There is a direct mapping between ticks and prices in Uni v3:

Price=1.0001TickPrice = 1.0001 ^ {Tick}

img-3

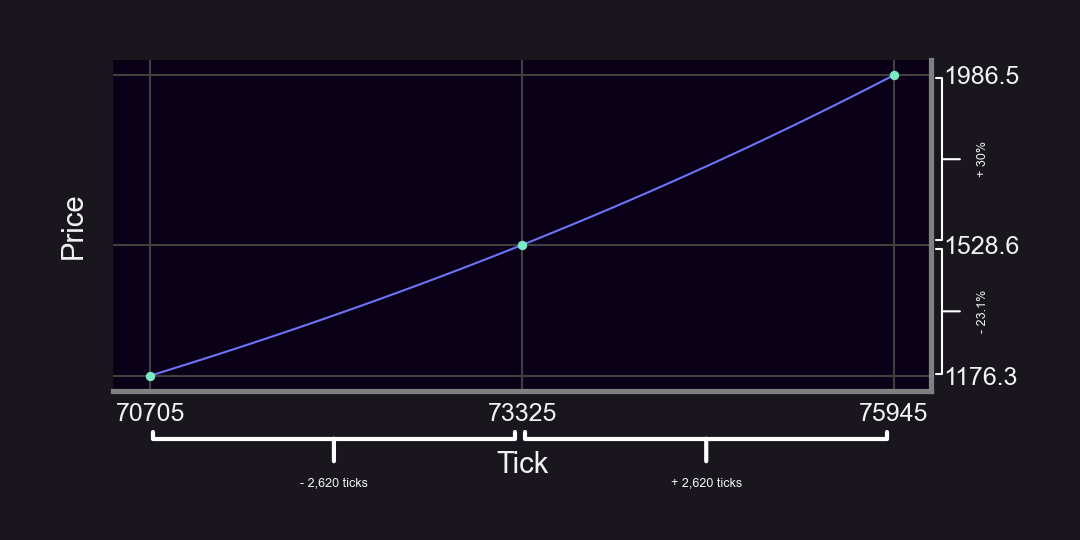
A price of $1,528 corresponds to tick 73,325 (since 1.000173,325≈$1,5281.0001 ^ {73,325} ≈ \$1,528).

If we LP on tick 73,325 with ±2,620 ticks, we get:

  • Lower: 1.000173,325−2,620≈$1,176\text{Lower: } 1.0001 ^ {73,325 - 2,620} ≈ \$1,176
  • Upper: 1.000173,325+2,620≈$1,986\text{Upper: } 1.0001 ^ {73,325 + 2,620} ≈ \$1,986

Key Insights:

  1. The math is ±ticks, not ±%. This generalizes to any LP range.
  2. For any LP Strategy of width ±X% (we used X = 30%), the proper price range to fully utilize capital is:
    • Lower: PX100+1\text{Lower: } \frac{P}{\frac{X}{100} + 1}
    • Upper: P×(X100+1)\text{Upper: } P \times (\frac{X}{100} + 1)

Caveats/Questions:

  • Don’t forget to leave some tokens to pay for gas (e.g. ETH on Ethereum, MATIC on Polygon).
  • How well do ±X% LP strategies perform?
  • What is a good X to pick?­

Disclaimer: This content is for educational purposes only and should not be relied upon as financial advice.